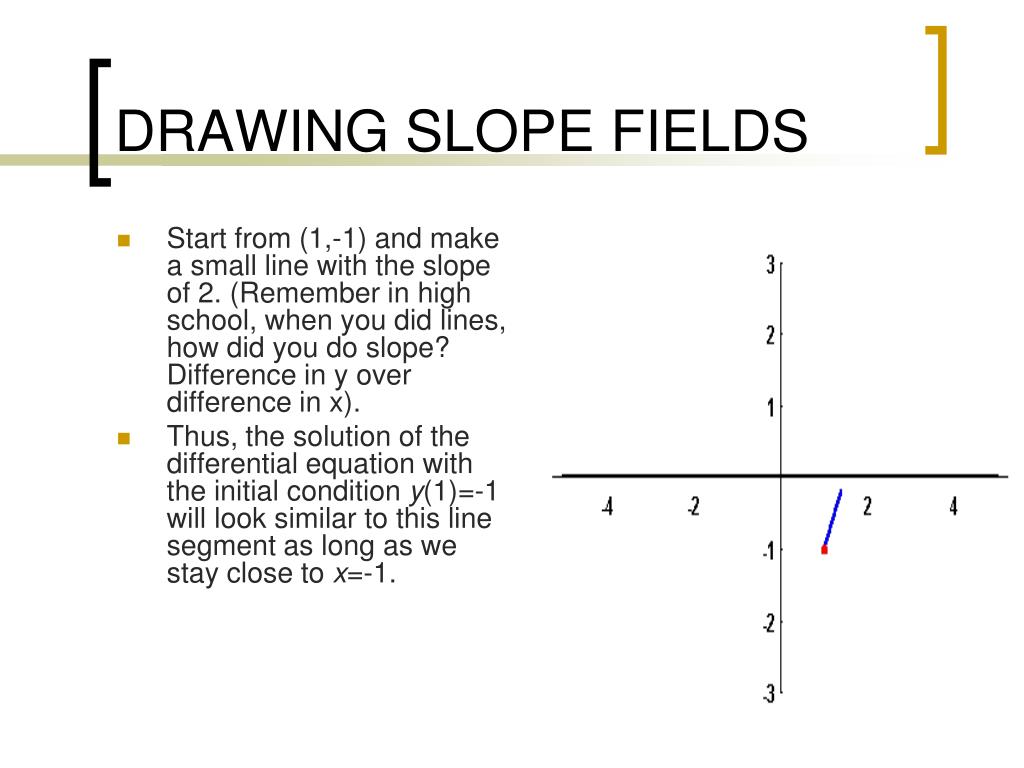
How To Draw Slope Fields

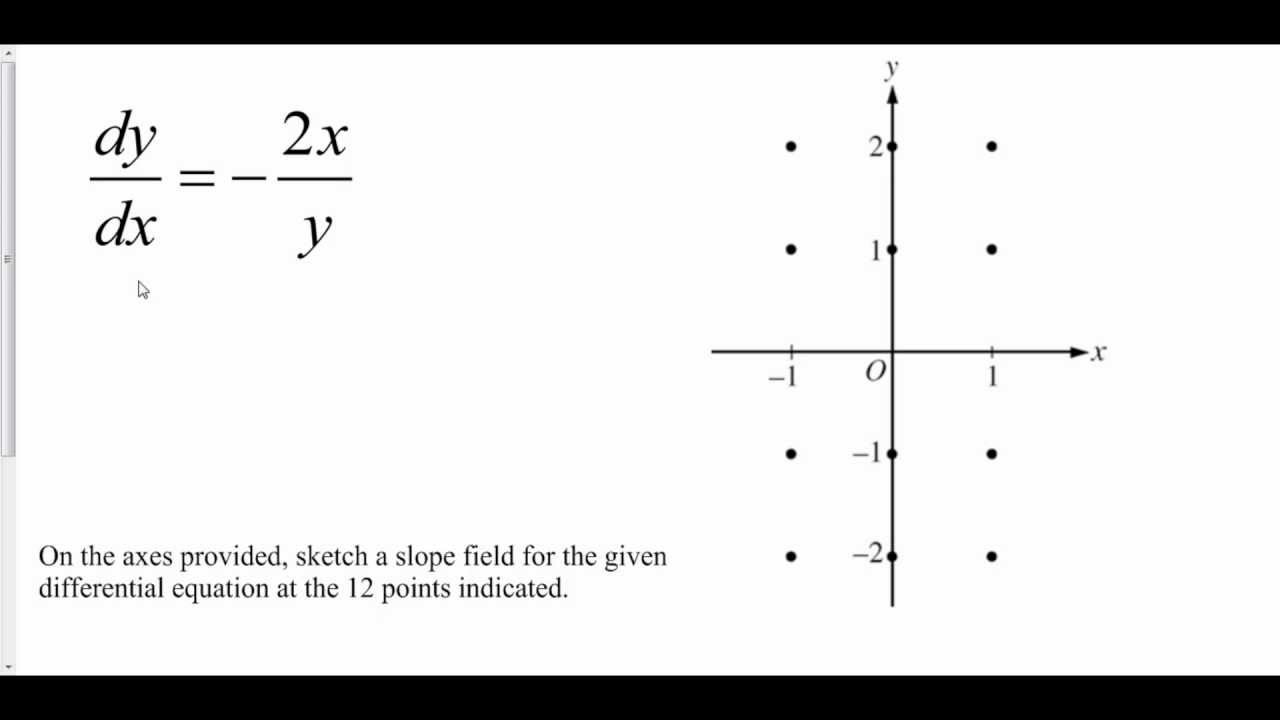
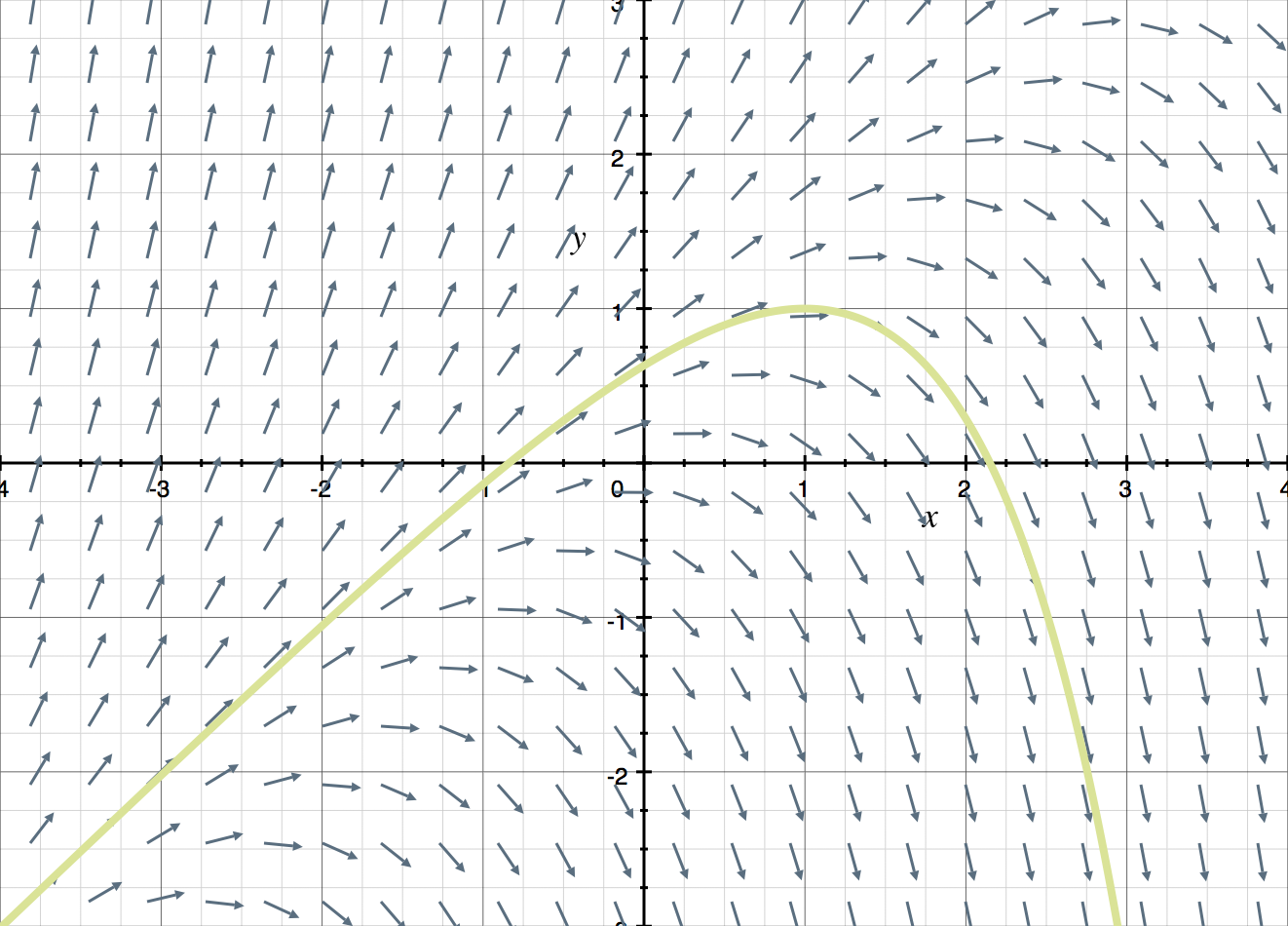
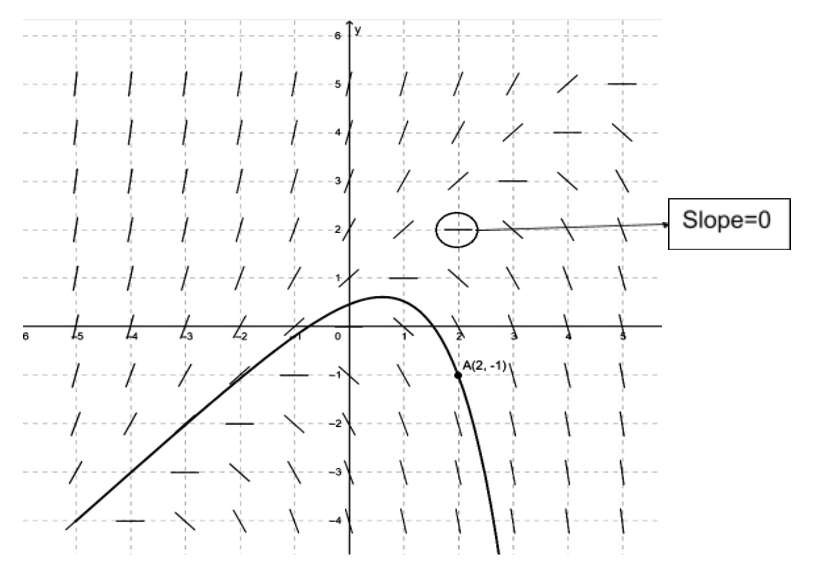
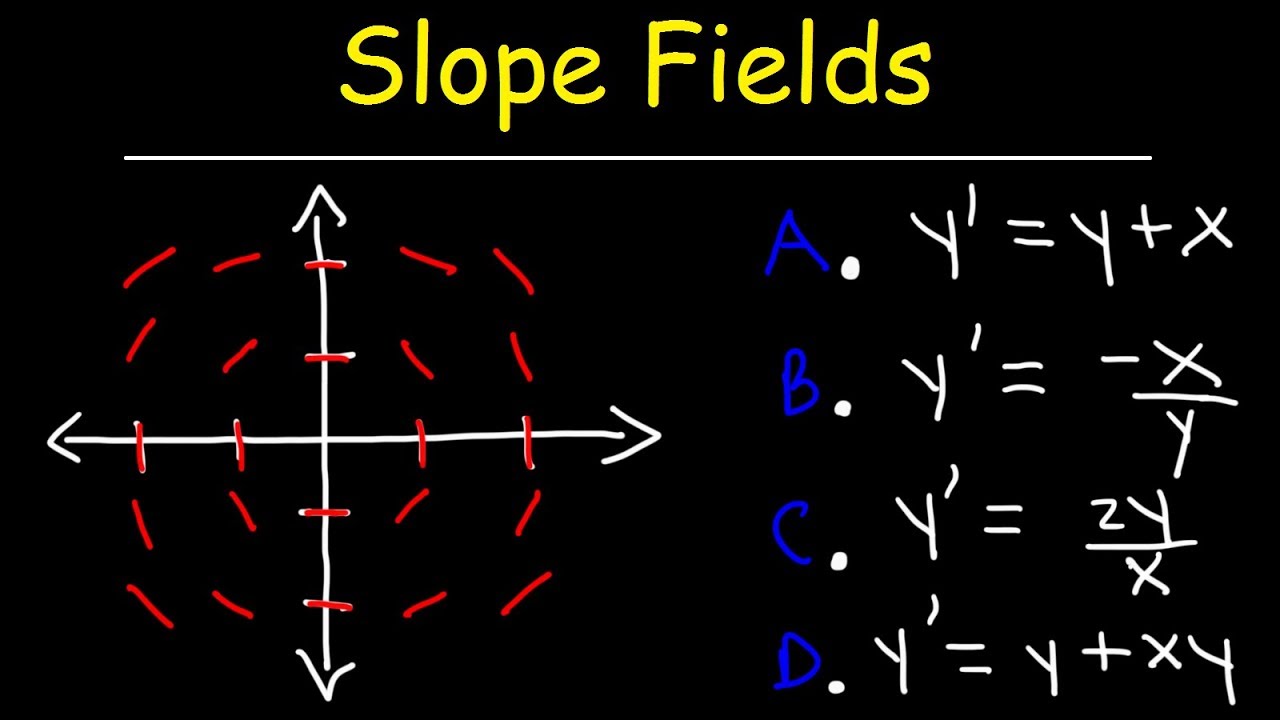
How To Draw Slope Fields - The pattern produced by the slope field aids in visualizing the shape of the curve of the solution. The slope field is a cartesian grid where you draw lines in various directions to represent the slopes of the tangents to the solution. Take the example of dy/dx at (3, 4). Web individual exploration with a computer graphing application is highly recommended. Web plot a direction field for a specified differential equation and display particular solutions on it if desired. We'll learn in a few sections how to solve this kind of equation, but for now we can't get an explicit solution. D y d x = x + y. D y d x = y − x. Therefore by drawing a curve through consecutive slope lines, you can find a solution to the differential equation. Web in this video, i will show you how to draw a slope field, also known as the direction field, which can be drawn from a differential equation y' = f (x,y).

D y d x = − x y. Web the slope field is a cartesian grid where you draw lines in various directions to represent the slopes of the tangents to the solution. The slope field is a cartesian grid where you draw lines in various directions to represent the slopes of the tangents to the solution. Take the example of dy/dx at (3, 4). Web given a slope field and a few differential equations, we can determine which equation corresponds to the slope field by considering specific slopes. Slope fields are tools used to graphically obtain the solutio. See how we match an equation to its slope field by considering the various slopes in the diagram. That's the slope field of the equation. We'll learn in a few sections how to solve this kind of equation, but for now we can't get an explicit solution. Web a slope ﬁeld of a differential equation gives a picture of the general behavior of the possible solutions to that differential equation, at least in the region covered by that slope ﬁeld.

Web given a slope field and a few differential equations, we can determine which equation corresponds to the slope field by considering specific slopes. Web the graph of a differential equation is a slope field. Slope fields are tools used to graphically obtain the solutio. This required evaluating the slope at that point, but that is simple since you are actually given the slope: Take the example of dy/dx at (3, 4). At a point $(x,y)$, we plot a short line with the slope $f. And this is the slope a solution \(y(x)$ would have at $x$ if its value was $y$. Web practice this lesson yourself on khanacademy.org right now: We'll illustrate this with a simple example: Web given a differential equation in x and y, we can draw a segment with dy/dx as slope at any point (x,y).

Graphing Slope Fields from a Differential Equation YouTube

A first derivative expressed as a function of x and y gives the slope of the tangent line to the solution curve that goes through any point in the plane. That's the slope field of the equation. Slope fields are tools used to graphically obtain the solutio. In other words, $f(x,y)$ is the slope of a solution whose graph runs.

How to sketch direction fields — Krista King Math Online math help

Web graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more. See how we match an equation to its slope field by considering the various slopes in the diagram. Web in this video, i will show you how to draw a slope field, also known as the direction field, which can be drawn from a differential equation.

$How do you draw the slope field of the differential equation \\[{{y$

How do you draw the slope field of the differential equation \\[{{y

Web in this video, i will show you how to draw a slope field, also known as the direction field, which can be drawn from a differential equation y' = f (x,y). D y d x = x y. Given a differential equation in x and y, we can draw a segment with dy/dx as slope at any point (x,y)..

How To Draw Directional Fields » Cookstrain

Web learn how to create slope fields and sketch the particular solution to a differential equation. D y d x = − x y. Then i hand them a sheet of grid paper and a ruler, and we start with a differential equation such as dy/dx = 2. Web slope fields & equations. In other words, $f(x,y)$ is the slope.

PPT DIFFERENTIAL EQUATIONS PowerPoint Presentation, free download

Sketch the slope field and sketch the particular equation YouTube

D y d x = x y. Web when i teach my students to draw a slope field, i first review how to graph a line, given a point and a slope. Learn how to draw them and use them to find particular solutions. Take the example of dy/dx at (3, 4). We'll illustrate this with a simple example:

Slope Fields • [6.1b] AP CALCULUS YouTube

The slope field is a cartesian grid where you draw lines in various directions to represent the slopes of the tangents to the solution. In other words, $f(x,y)$ is the slope of a solution whose graph runs through the point $(x,y)$. Web practice this lesson yourself on khanacademy.org right now: Web slope fields & equations. The pattern produced by the.

How To Draw Directional Fields » Cookstrain

D y d x = − x y. And this is the slope a solution $y(x)$ would have at $x$ if its value was $y$. Take the example of dy/dx at (3, 4). Web in this video, i will show you how to draw a slope field, also known as the direction field, which can be drawn from a differential.

PPT Slope Fields PowerPoint Presentation, free download ID5878177

Then i hand them a sheet of grid paper and a ruler, and we start with a differential equation such as dy/dx = 2. Web this calculus video tutorial provides a basic introduction into slope fields. D y d x = y − x. We'll illustrate this with a simple example: The slope field is a cartesian grid where you.

Differential Equations How to Draw slope fields YouTube

The pattern produced by the slope field aids in visualizing the shape of the curve of the solution. D y d x = x y. Y' = t + y y′ = t + y. Web practice this lesson yourself on khanacademy.org right now: Then i hand them a sheet of grid paper and a ruler, and we start with.

Y′ = Y1 + Y 1 + X Y ′ = Y 1 + Y 1 + X.

Web plot a direction field for a specified differential equation and display particular solutions on it if desired. Web when i teach my students to draw a slope field, i first review how to graph a line, given a point and a slope. A first derivative expressed as a function of x and y gives the slope of the tangent line to the solution curve that goes through any point in the plane. Slope fields make use of this by imposing a grid of points evenly spaced across the cartesian plane.

See How We Match An Equation To Its Slope Field By Considering The Various Slopes In The Diagram.

Web a slope ﬁeld of a differential equation gives a picture of the general behavior of the possible solutions to that differential equation, at least in the region covered by that slope ﬁeld. D y d x = x − y. Web individual exploration with a computer graphing application is highly recommended. Web we can plot a slope field like this, not too much trouble if we essentially just keep solving for the slopes, and then we can use that slope field to get a conceptual or visual understanding of what the solutions might look like given points that the solutions might actually contain.

Web The Graph Of A Differential Equation Is A Slope Field.

Which differential equation generates the slope field? D y d x = x y. Learn how to draw them and use them to find particular solutions. D y d x = y − x.

Clearly, T T Is The Independent Variable, And Y Y Is A Function Of T.

Web the slope field is a cartesian grid where you draw lines in various directions to represent the slopes of the tangents to the solution. Therefore by drawing a curve through consecutive slope lines, you can find a solution to the differential equation. Y' = t + y y′ = t + y. D y d x = x − y.