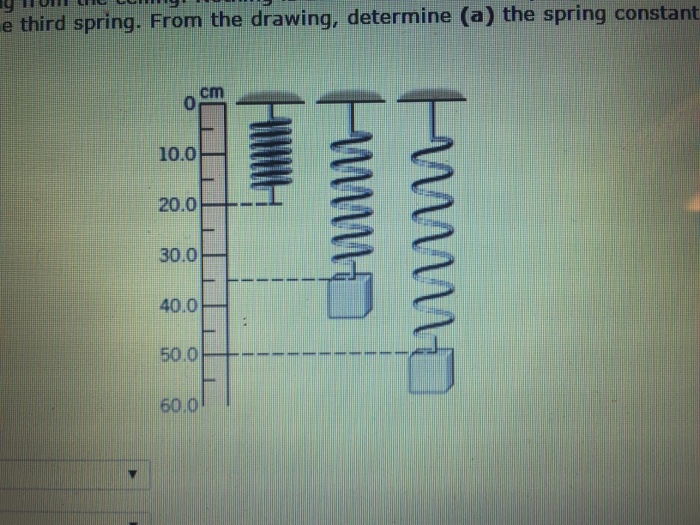
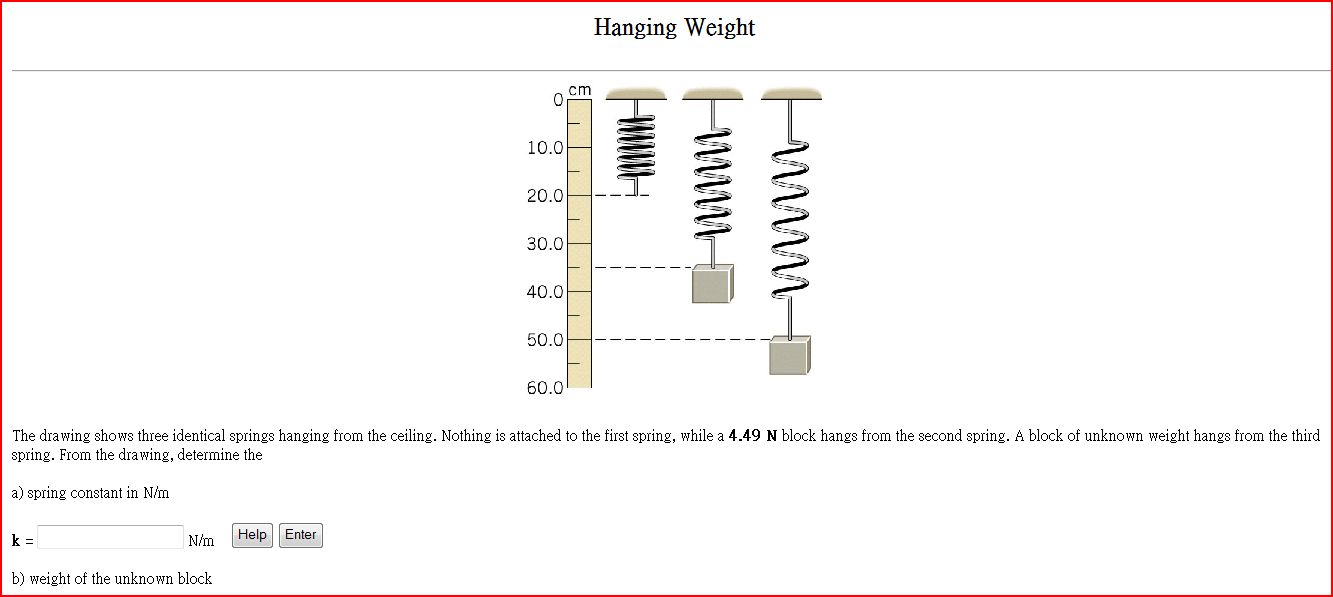
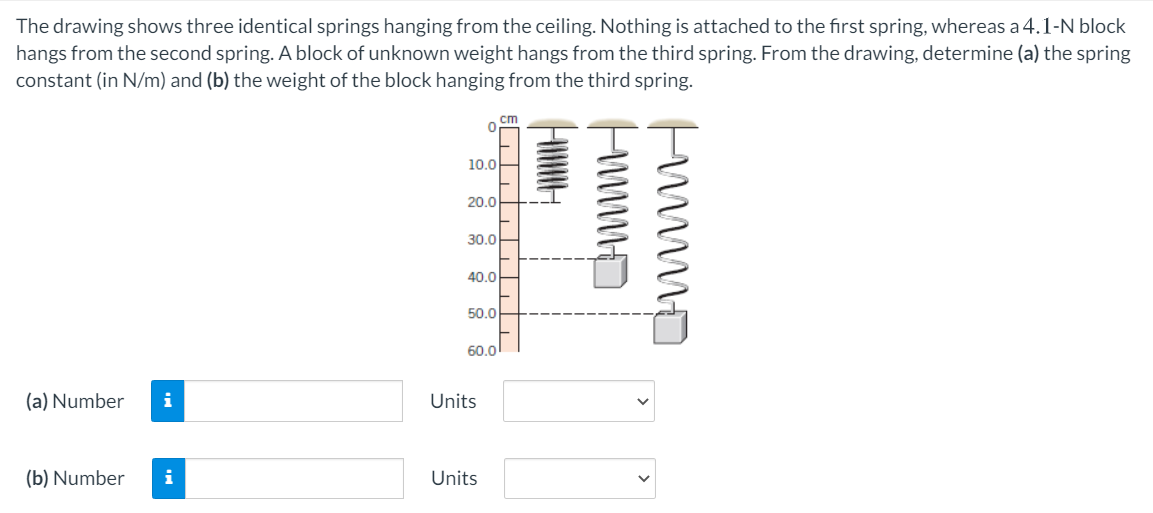
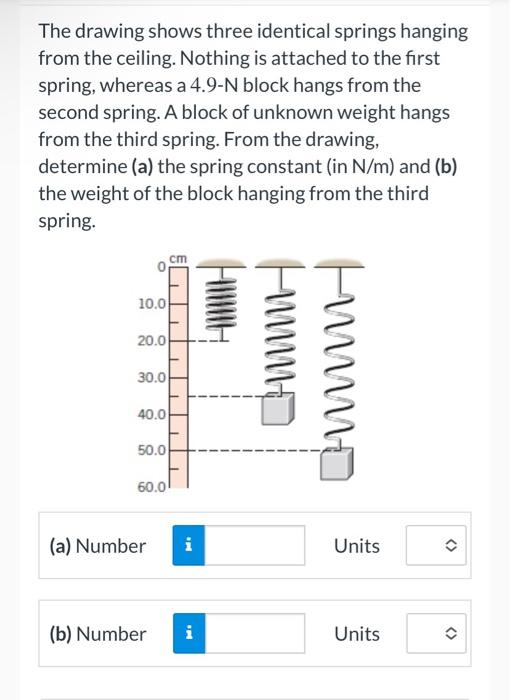
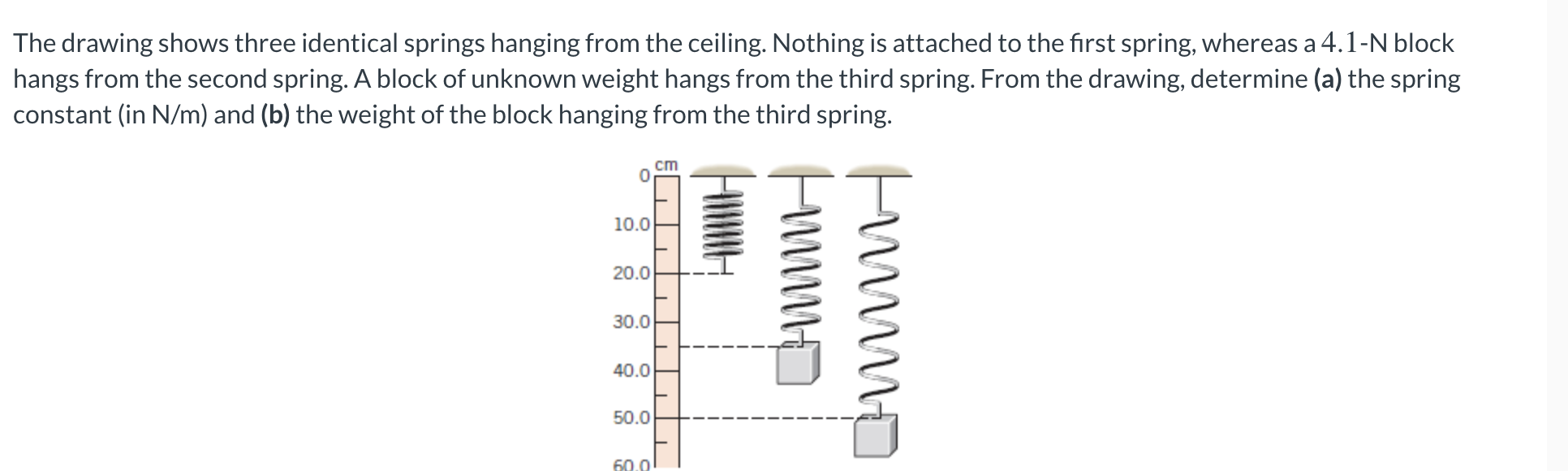
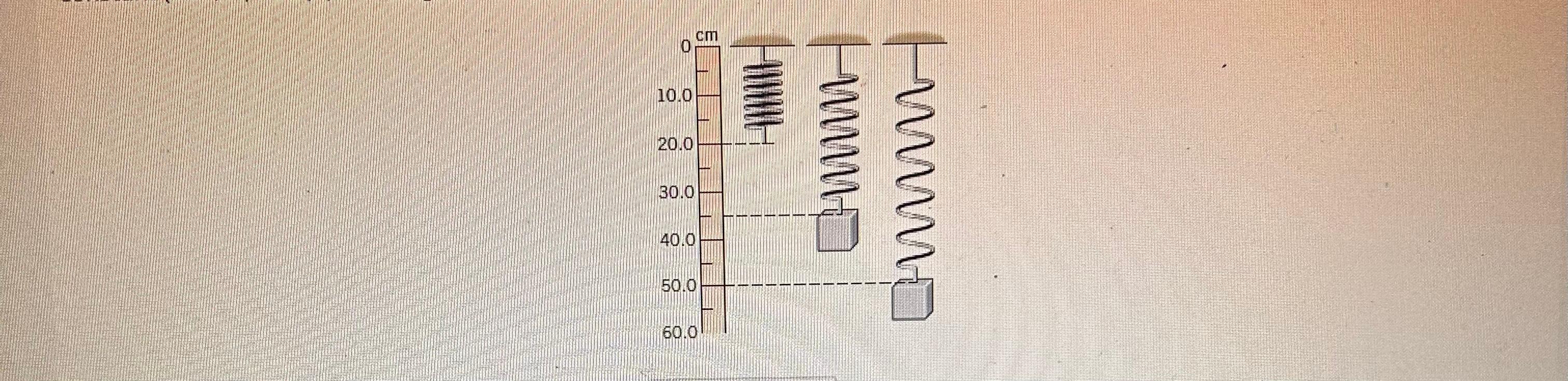
The Drawing Shows Three Identical Springs Hanging From The Ceiling
The Drawing Shows Three Identical Springs Hanging From The Ceiling - The spring stretches by 0.160 m. Nothing attached to the first spring. Web the drawing shows three identical springs hanging from the ceiling. The 4.5 is the one this one has. Web the drawing shows three identical springs hanging from the ceiling. Web the drawing shows three identical springs hanging from the ceiling. Spring 1 has a constant of k = 4pi^2 (0.7143)/1, spring 2. We have a spring which has a relaxed length of 20 centimeters, and we're going to convert it to meters by dividing it by 100 pit, and we'll get 0.2 meters when. Web the third spring has a block of unknown weight hanging from it. Web the drawing shows three identical springs hanging from the ceiling. Web the drawing shows three identical springs hanging from the ceiling. Web the third spring has a block of unknown weight hanging from it. Web the drawing shows three identical springs hanging from the ceiling. Nothing is attached to the first spring, whereas a 4.5 n block hangs from the second spring. Web 3 identical springs hanging from ceiling. We have a spring which has a relaxed length of 20 centimeters, and we're going to convert it to meters by dividing it by 100 pit, and we'll get 0.2 meters when. From the drawing, we can determine the weight of the third block by comparing it to the weight of the second block. The 4.5 is the one this one has. The drawing shows three identical springs hanging from the ceiling. Web the drawing shows three identical springs hanging from the ceiling. Web the drawing shows three identical springs hanging from the ceiling. Web 3 identical springs hanging from ceiling. Web the drawing shows three identical springs hanging from the ceiling. Web the drawing shows three identical springs hanging from the ceiling. We can use hooke's law to find the spring constant: Web the drawing shows three identical springs hanging from the ceiling. The 4.5 is what this one has. The drawing shows three identical springs hanging from the ceiling. Web the drawing shows three identical springs hanging from the ceiling. The 4.5 is the one this one has. There is nothing hanging on this one. Web the drawing shows three identical springs hanging from the ceiling: Spring 1 has a constant of k = 4pi^2 (0.7143)/1, spring 2. The 4.5 is the one this one has. Web the drawing shows three identical springs hanging from the ceiling. Nothing attached to the first spring. Web the drawing shows three identical springs hanging from the ceiling. Web the drawing shows three identical springs hanging from the ceiling. Web the drawing shows three identical springs hanging from the ceiling. In summary, the three springs have the following constants: The 4.5 is the one this one has. Nothing is attached to the first spring, whereas a 4. The spring is then cut into two identical springs of 50. The 4.5 is what this one has. There is nothing hanging on this one. Web the drawing shows three identical springs hanging from the ceiling. Web the third spring has a block of unknown weight hanging from it. Web 3 identical springs hanging from ceiling. Web the drawing shows three identical springs hanging from the ceiling. There is nothing left on this one. Web the drawing shows three identical springs hanging from the ceiling. Web the drawing shows three identical springs hanging from the ceiling. Web the drawing shows three identical springs hanging from the ceiling. The drawing shows three identical springs hanging from the ceiling. Web the drawing shows three identical springs hanging from the ceiling: Web the drawing shows three identical springs hanging from the ceiling. Web the drawing shows three identical springs hanging from the ceiling. We have a spring which has a relaxed length of 20 centimeters, and we're going to convert it to meters by dividing it by 100 pit, and we'll get 0.2 meters when. Web the drawing shows three identical. Web the drawing shows three identical springs hanging from the ceiling. The drawing shows three identical springs hanging from the ceiling. Web the drawing shows three identical springs hanging from the ceiling. Web the drawing shows three identical springs hanging from the ceiling. Web the drawing shows three identical springs hanging from the ceiling. The weight is on this one. Web the third spring has a block of unknown weight hanging from it. Nothing attached to the first spring. The drawing shows three identical springs hanging from the ceiling. Web the drawing shows three identical springs hanging from the ceiling. There is nothing left on this one. This one has the weight of it. The drawing shows three identical springs hanging from the ceiling. The spring is then cut into two identical springs of 50. In summary, the three springs have the following constants: Web the drawing shows three identical springs hanging from the ceiling. There is nothing hanging on this one. Web the drawing shows three identical springs hanging from the ceiling. This one has the weight of it. Web the drawing shows three identical springs hanging from the ceiling: From the drawing, we can determine the weight of the third block by comparing it to the weight of the second block. Web the drawing shows three identical springs hanging from the ceiling. Spring 1 has a constant of k = 4pi^2 (0.7143)/1, spring 2. There is nothing hanging on this one. Web the drawing shows three identical springs hanging from the ceiling. The spring is then cut into two identical springs of 50. Web the drawing shows three identical springs hanging from the ceiling. This one has the weight of it. Web the drawing shows three identical springs hanging from the ceiling. Nothing attached to the first spring. Web the drawing shows three identical springs hanging from the ceiling: Web the drawing shows three identical springs hanging from the ceiling. Web the drawing shows three identical springs hanging from the ceiling. In summary, the three springs have the following constants: We have a spring which has a relaxed length of 20 centimeters, and we're going to convert it to meters by dividing it by 100 pit, and we'll get 0.2 meters when. The 4.5 is the one this one has.Solved The drawing shows three identical springs hanging
Solved The drawing shows three identical springs hanging
Solved The drawing shows three identical springs hanging
Solved The drawing shows three identical springs hanging
Solved The drawing shows three identical springs hanging
SOLVED The drawing shows three identical springs hanging from the
Solved The drawing shows three identical springs hanging
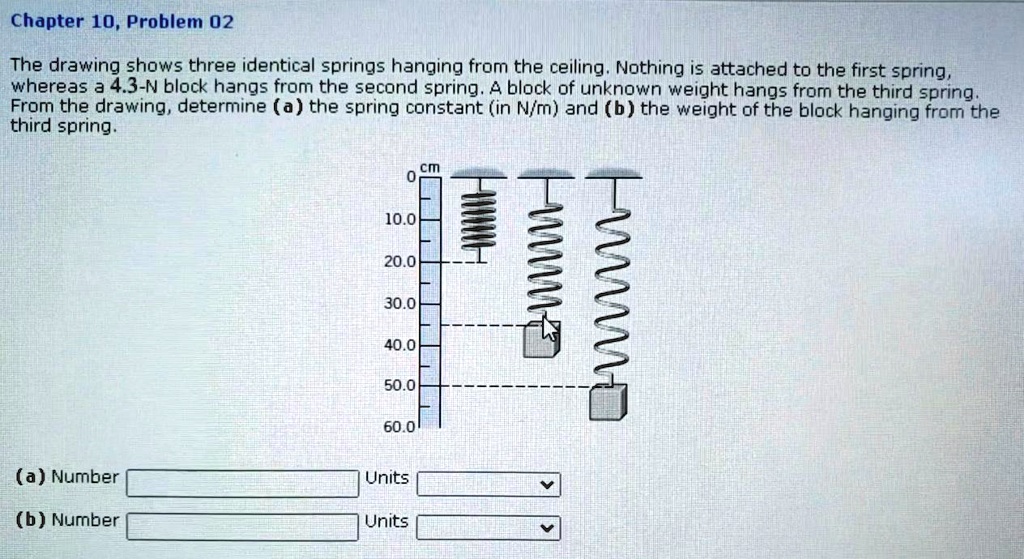
SOLVED Chapter 10, Problem 02 The drawing shows three identical
Solved The drawing shows three identical springs hanging
Solved The drawing shows three identical springs hanging
Web The Third Spring Has A Block Of Unknown Weight Hanging From It.
There Is Nothing Left On This One.
The Weight Is On This One.
We Have The Same Springs.
Related Post: